|
017..:: 08.04.2011

..:: Del Buono Corrado.
CASATENOVO - LC ..:: Nel progettare una attività didattica
gli insegnanti devono predisporre lavori che consentano
all’alunno di acquisire, contestualmente, sia gli aspetti
teorici della disciplina, sia abilità operative spendibili
in altre materie di studio o nel mondo del lavoro. Queste
ultime possono essere sviluppate attraverso esercitazioni
pratiche mirate, da svolgersi con l’ausilio della lavagna
interattiva. Le esercitazioni pratiche possono avere come
riferimento aspetti teorici o anche abilità già acquisite
dagli studenti; dove possibile, l’insegnante dovrebbe
preferire questa seconda alternativa perché facilita
l’apprendimento da parte dell’allievo in quanto è già in
grado di svolgere, almeno in parte, il compito assegnatogli.
Le esercitazioni pratiche costruite sul bagaglio di
esperienza degli alunni, inoltre, consentono loro, di
comprendere che le abilità acquisite in una fase precedente
del percorso formativo, sono utili per cercare soluzioni a
nuovi problemi.
ESEMPIO DI PROGETTAZIONE DI UNA UNITA’ DIDATTICA CON
WORKSPACE.
Facciamo un esempio su come progettare una attività
didattica che tragga spunto da conoscenze ed abilità
pregresse.
Supponiamo di dover affrontare una lezione di matematica sul
calcolo dell'area di un trapezio. Di solito, tale argomento
si affronta dopo aver studiato le figure piane del
rettangolo e del triangolo; pertanto, poiché gli alunni
hanno già conoscenze ed abilità che permettono loro di
risolvere il nuovo problema, possiamo far calcolare l’area
del trapezio come somma delle aree dei due triangoli e del
rettangolo centrale, e solo successivamente, introdurre la
formula per il calcolo dell’area del trapezio. Gli alunni ne
determineranno il valore e lo confronteranno con quello
calcolato in precedenza.
SRUTTURARE UNA ATTIVITA’ CON WORKSPACE.
Vediamo, operativamente, come strutturare una simile
attività su di un foglio di Workspace. Iniziamo con
l’inserire una cornice di testo per il titolo, attraverso il
pulsante TESTO posto sulla barra degli strumenti. Digitiamo
al suo interno “Calcolo dell’area di un trapezio”,
formattiamo il titolo e posizioniamolo nella parte alta del
foglio.
Creiamo, con lo strumento FORME, un rettangolo che occupi
l’area sinistra del foglio di lavoro assegnando ad esso un
bordo di medie dimensioni e di colore verde; creiamo,
utilizzando la stessa formattazione, altri due rettangoli
nella parte destra del foglio. Nel rettangolo di dimensioni
maggiori disegniamo un trapezio; poiché tale forma non è
presente tra gli strumenti di Workspace, assembliamo due
triangoli con un rettangolo utilizzando la stessa
formattazione per le tre forme. Assegniamo a queste ultime
una etichetta, ad esempio A, B e C.
Nel rettangolo posto in alto nella destra creiamo delle
etichette, seguite da puntini, per guidare nel calcolo,
l’alunno che dovrà svolgere l’esercizio.
Inseriamo una cornice di testo e digitiamo, su tre righe,
rispettivamente AREA DEL TRIANGOLO A, AREA DEL RETTANGOLO B
e AREA DEL TRIANGOLO C.
Sulla quarta riga digitiamo, infine, AREA DEL TRAPEZIO
(A+B+C).
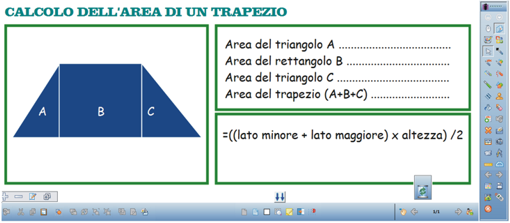
Nel secondo riquadro dobbiamo inserire la formula
matematica per il calcolo dell’area del trapezio. Poiché
tale formula dovrà essere mostrata ai ragazzi solo in un
secondo momento, andremo a trascriverla su di un nuovo
livello che verrà nascosto, inizialmente, alla classe.
Creiamo, quindi, attraverso il pulsante AGGIUNGI LIVELLO, un
nuovo livello e rinominiamolo in FORMULA. Inseriamo, in
corrispondenza del secondo rettangolo posto in basso sulla
destra del foglio di lavoro, una cornice di testo con la
formula, ovvero, ((LATO MINORE + LATO MAGGIORE)*ALTEZZA)/2.
Nascondiamo il livello aggiuntivo contenente la formula
dell’area del trapezio e creiamo un ulteriore livello sul
quale gli alunni andranno ad eseguire i loro calcoli.
Il lavoro è pronto. Possiamo salvare il file ed utilizzarlo
in classe.
Vediamo, ora, le procedure operative da seguire per svolgere
l’attività didattica in classe. L’alunno chiamato alla
lavagna, dovrà utilizzare lo STRUMENTO RIGHELLO e scegliere
uno dei due disponibili, ad esempio quello METRICO.
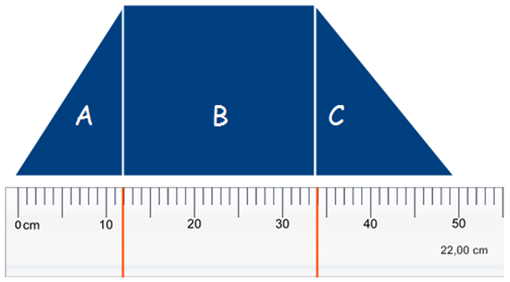
Calcolerà, aiutandosi con le linee guida di colore rosso
poste sul righello, la lunghezza della base dei due
triangoli e del rettangolo, e scriverà tali valori nella
cornice predisposta in precedenza.
Ruoterà il righello per determinare l’altezza del trapezio
ed inserirà tale valore, sempre nella cornice di testo.
Procederà successivamente nel calcolo dell’area del trapezio
come somma delle aree dei due triangoli e del rettangolo.
A questo punto, l’insegnante mostrerà la formula
dell’area del trapezio, attivando il livello nascosto. Il
ragazzo calcolerà, attraverso quest’ultima formula, l’area
del trapezio e confronterà il risultato con quello
determinato in precedenza. L'insegnante si assicurerà che
l'alunno esegua i calcoli, sempre sull'ultimo livello del
foglio di Workspace. Al termine dell’esercizio, l'insegnante
potrà semplicemente nascondere il livello utilizzato dal
ragazzo, e crearne uno nuovo per un altro studente.
Ovviamente, dovrà avere l'accortezza di modificare la forma
del trapezio prima di far svolgere l'attività operativa
all'alunno chiamato alla lavagna.
Corrado Del Buono
webmaster@corradodelbuono.it


www.assodolab.it
|



















